I finished up a project the other day, so I gave myself a few minutes to make something just for fun. Here’s a grid of hexagonal tiles with little bits of graphics in them. Over time, random tiles rotate to create a new pattern (in this screenshot, you can see 5 tiles in mid-rotation). I played around with a whole bunch of different coloring schemes, and found that this combination of light and dark warm browns had just the right kind of feeling for me. Although it may look like the tiles are circular (a sensation that’s even stronger when you watch them rotate), they really are all hexagons. Read on for how I did this and the program itself.
Each hexagonal tile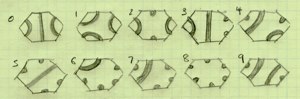 
has six sides, and each side has one bit of a “band” on each edge. I decided for simplicity that I didn’t want the internal bands to overlap. So how many different tiles can you draw with that constraint? Factoring out rotation and reflection, there are 10 types of tiles. It’s fun to think about these and make sure you’ve got them all. I drew these out on a piece of paper and gave each one a number, so I could type their descriptions into my program and I’d know which tile I meant at what position.
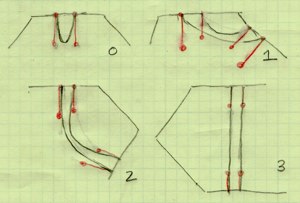There are just four different types of shapes inside these tiles: the little end-cap, the straight line that joins opposite sides, and the two curves that join neighboring sides, or sides with one side between them. I draw all of these with a pair of Bezier curves (joined by straight lines along the edges). I wanted the curves to be graceful and interesting, so I played with the locations of the Bezier knots until they looked good to me. This is one of the pleasures of this kind of programming: once the math is in place, you can just fiddle with the numbers intuitively until the picture feels right.
My program first populates the world with random tiles, though it tries to choose them so that we don’t get too many small closed loops. Then on every frame, I look at any tiles that have just finished rotating, and choose a neighbor to start rotating. The tiles spin at slightly different speeds, so they start and stop at different times. It’s fun to watch the evolving patterns.
Here’s the code. I haven’t cleaned it up or tried to make it really nice – this was just a little fun project, after all, and I didn’t intend to share it. Think of this as a rough draft. There are two files: rotatingHexTiles.pde is the main project. Tile.pde holds the Tile class.
rotatingHexTiles.pde:
// rotating hexagon tiles, version 1.0
// (c) 2013 Andrew Glassner
Tile[] TileList;
// These are the 10 different types of tiles. Codes:
// -1 = nothing "starts" at this edge
// 0 = end cap (or half a dot)
// 1 = connects to next edge clockwise
// 2 = connects to edge that's two edges clockwise
// 3 = connects to edge opposite this one
int[][] Styles = {
{ -1, 3, 1, -1, -1, 1 },
{-1, 1, -1, 1, -1, 1 },
{ 0, 1, -1, 0, 1, -1 },
{-1, 3, 0, 0, -1, 1 },
{ -1, 0, 1, -1, 2, 0 },
{ 0, 3, 0, 0, -1, 0 },
{ -1, 0, 0, 0, 0, 1 },
{-1, 0, 0, 0, 2, 0 },
{ 0, 0, 0, 0, 0, 0 },
{ -1, 2, 0, -1, 2, 0 }
};
int NumX, NumY;
int RotateDurationRangeStart = 20;
int RotateDurationRangeEnd = 50;
void setup() {
size(800, 800);
float r = 40;
float h = r/Cos30;
float s2 = h*Sin30;
float s = 2*s2;
NumX = int(1+(2*ceil(width*1.0/(h+s2))));
NumY = int(1+(ceil(height*1.0/(2*r))));
TileList = new Tile[NumX*NumY];
for (int y=0; y<NumY; y++) {
for (int x=0; x<NumX; x++) {
float cx = x*(h+s2);
float cy = y*(2*r);
if (x%2 == 1) cy += r;
int index = (y*NumX)+x;
int whichStyle = int(random(0,2));
boolean hasDots = random(0,1) > .5;
if (hasDots) whichStyle = int(random(2,10));
TileList[index] = new Tile(cx, cy, r, int(random(0,6))*PI/3,
color(240,233,205), Styles[whichStyle]);
boolean doChange = random(0, 1) > .95;
if (doChange) {
int stopFrame = int(random(RotateDurationRangeStart,
RotateDurationRangeEnd));
TileList[index].startChange(0, stopFrame, random(0,1)>.5, Styles[0]);
}
}
}
}
void draw() {
background(195,155,135);
for (int i=0; i<TileList.length; i++) {
TileList[i].render();
// if this tile just stopped rotating, start up a neighbor
if (TileList[i].justStoppedChanging) {
int thisY = int(i*1.0/NumY);
int thisX = i-(thisY*NumX);
int offset = int(random(0,4));
for (int j=0; j<4; j++) {
int newIndex = -1;
int whichCase = (j+offset)%4;
switch (whichCase) {
case 0:
if (thisX > 0) newIndex = (thisY*NumX)+(thisX-1);
break;
case 1:
if (thisX < NumX-1) newIndex = (thisY*NumX)+(thisX+1);
break;
case 2:
if (thisY > 0) newIndex = ((thisY-1)*NumX)+thisX;
break;
case 3:
if (thisY < NumY-1) newIndex = ((thisY+1)*NumX)+thisX;
break;
}
if (newIndex >= 0) {
if (!TileList[newIndex].changing) {
int stopFrame = frameCount+int(random(RotateDurationRangeStart,
RotateDurationRangeEnd));
TileList[newIndex].startChange(frameCount, stopFrame,
random(0,1)>.5, Styles[0]);
break;
}
}
}
}
}
}
Tile.pde:
// A class for a hexagonal tile with an internal pattern, version 1.0
// (c) 2013 Andrew Glassner
float Sin30 = .5;
float Cos30 = cos(radians(30));
float Sin60 = Cos30;
float Cos60 = .5;
class Tile {
float cx, cy, r, s, s2, h;
int[] ecode;
float barWeight;
color strokeColor;
float spinAngle;
float bezD;
boolean changing, justStoppedChanging;
int changeStartFrame, changeStopFrame;
boolean changeClockwise;
int[] changeEcode;
Tile(float tx, float ty, float tr, float rotationAngle,
color c, int[] edgeStyle) {
cx = tx;
cy = ty;
r = tr;
h = r/Cos30;
s2 = h*Sin30;
s = 2*s2;
bezD = h*.6;
spinAngle = rotationAngle;
strokeColor = c;
ecode = new int[6];
for (int i=0; i<6; i++) ecode[i] = edgeStyle[i];
barWeight = .125 * (h/Sin30);
changing = false;
justStoppedChanging = false;
changeEcode = new int[6];
}
void startChange(int startFrame, int stopFrame,
boolean clockwise, int[] newcode) {
changeStartFrame = startFrame;
changeStopFrame = stopFrame;
changeClockwise = clockwise;
for (int i=0; i<6; i++) changeEcode[i] = newcode[i];
changing = true;
}
PVector lerpPVector(PVector a, PVector b, float alfa) {
PVector c = new PVector(lerp(a.x, b.x, alfa), lerp(a.y, b.y, alfa));
return(c);
}
float ease(float x) {
return(map(cos(PI*x), 1, -1, 0, 1));
}
void render() {
float blendNear = (s2-barWeight/2.0)/s;
float blendFar = (s2+barWeight/2.0)/s;
PVector ul = new PVector(-s2, -r);
PVector ur = new PVector( s2, -r);
PVector mr = new PVector( h, 0);
PVector lr = new PVector( s2, r);
PVector ll = new PVector(-s2, r);
PVector pA0 = lerpPVector(ul, ur, blendNear);
PVector pB0 = lerpPVector(ul, ur, blendFar);
PVector pC0 = lerpPVector(ur, mr, blendNear);
PVector pD0 = lerpPVector(ur, mr, blendFar);
PVector pE0 = lerpPVector(mr, lr, blendNear);
PVector pF0 = lerpPVector(mr, lr, blendFar);
PVector pG0 = lerpPVector(lr, ll, blendNear);
PVector pH0 = lerpPVector(lr, ll, blendFar);
PVector pA1 = new PVector(pA0.x, pA0.y+bezD);
PVector pB1 = new PVector(pB0.x, pB0.y+bezD);
PVector pC1 = new PVector(pC0.x - (bezD*Cos30), pC0.y + (bezD*Sin30));
PVector pD1 = new PVector(pD0.x - (bezD*Cos30), pD0.y + (bezD*Sin30));
PVector pE1 = new PVector(pE0.x - (bezD*Cos30), pE0.y - (bezD*Sin30));
PVector pF1 = new PVector(pF0.x - (bezD*Cos30), pF0.y - (bezD*Sin30));
PVector pG1 = new PVector(pG0.x, pG0.y-bezD);
PVector pH1 = new PVector(pH0.x, pH0.y-bezD);
justStoppedChanging = false;
for (int i=0; i<6; i++) {
pushMatrix();
translate(cx, cy);
rotate(i*PI/3);
if (changing) {
if (frameCount > changeStopFrame) {
changing = false;
justStoppedChanging = true;
if (changeClockwise) spinAngle += PI/3;
else spinAngle -= PI/3;
} else {
float theta = map(frameCount, changeStartFrame,
changeStopFrame, 0, 1);
theta = (PI/3)*ease(theta);
theta = min(theta, PI/3);
if (!changeClockwise) theta = -theta;
rotate(theta);
}
}
rotate(spinAngle);
stroke(strokeColor);
fill(strokeColor);
strokeWeight(1);
//line(-s2, -r, s2, -r);
beginShape();
switch (ecode[i]) {
case 0:
vertex(pA0.x, pA0.y);
bezierVertex(pA1.x, pA1.y, pB1.x, pB1.y, pB0.x, pB0.y);
break;
case 1:
case 5:
if (ecode[i] == 5) rotate(-TWO_PI/6);
vertex(pA0.x, pA0.y);
bezierVertex(pA1.x, pA1.y, pD1.x, pD1.y, pD0.x, pD0.y);
vertex(pC0.x, pC0.y);
bezierVertex(pC1.x, pC1.y, pB1.x, pB1.y, pB0.x, pB0.y);
break;
case 2:
case 4:
if (ecode[i] == 4) rotate(-TWO_PI/3);
vertex(pA0.x, pA0.y);
bezierVertex(pA1.x, pA1.y, pF1.x, pF1.y, pF0.x, pF0.y);
vertex(pE0.x, pE0.y);
bezierVertex(pE1.x, pE1.y, pB1.x, pB1.y, pB0.x, pB0.y);
break;
case 3:
vertex(pA0.x, pA0.y);
vertex(pH0.x, pH0.y);
vertex(pG0.x, pG0.y);
vertex(pB0.x, pB0.y);
break;
default:
}
endShape(CLOSE);
popMatrix();
}
}
}
Pingback: Projet vjing | Pearltrees