Given a circle of radius r, and around it a box of side 2r. We want to put another circle into the gap between the circle and a corner of the box. Find a formula for the center and radius of the largest circle that can be fit into that space. This might be a little trickier than you first think.

The solution’s after the break, but don’t give up too soon! 

They key thing is to not assume the circle is centered in the “middle” of the gap.

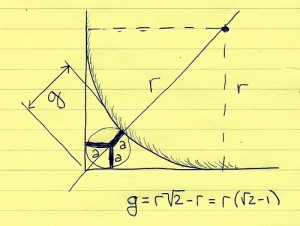
Symmetry says the circle must be on the diagonal. The radius we seek, which I’ll call a, makes the inner circle touch both edges of the box and the big circle; clearly no circle can be bigger. The diagonal of the square is r√2, so the piece of the diagonal in the gap is g = r (√2-1).

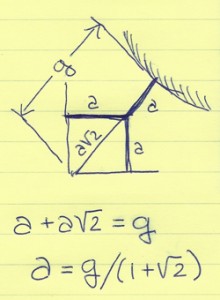
Focus on the little region in the bottom left. The line from the corner to the circle has length g. The upper part of the line has length a. The lower part is the diagonal of a box with side a, so that lower part has length a√2. Thus g = a + a√2, or a = g/(1+√2).

When I first worked this out I had all sorts of triangles and things floating around. I was definitely over-thinking it! The answer is nice and easy.

Note that this is basically an Appolonian gasket, but because we’re tangent to a circle and two perpendicular lines (rather than three circles) our result is a simple special case.