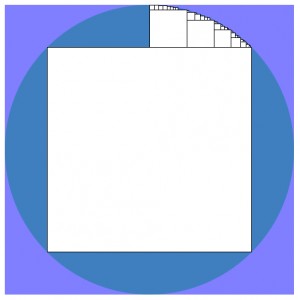
Here’s a fun algorithm: put the biggest possible square into a circle. Then looking at just the right side of the space above that square, add in the biggest possible square, then add in the biggest square into the space that remains, and so on, filling up that octant of the circle. It’s not too hard. My solution’s after the break.

Here’s how I did it. Suppose your circle is centered at (0,0) with radius r. Your first square is then centered at (0,0) as well, with “radius” r/√2 (here I’ll call the “radius” of a square the distance from its center to a midpoint of the edge – so it’s half the length of an edge).

Now write a little utility to intersect a line with a circle. The circle will always be our original circle (here shown in green), but the line will change. The routine should give you back the point of intersection (in this technique, such a point will always exist). It’s easy to derive the math for this routine, or you can find lots of ready-made implementations online.

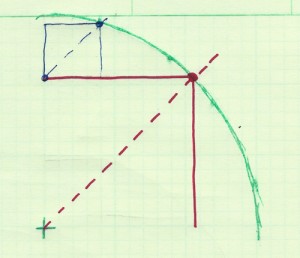We’re going to write an iterative algorithm that will create new squares based on existing ones, filling up one octant of the region between the square and the circle. You can fill in the other octants by symmetry (or you can compute them by making a tiny change to the algorithm). We need to “seed” the algorithm with a starting square that’s in the octant (the starting square isn’t useful because it’s in all eight octants). So create a line that starts at the midpoint of the top of the first square and extends up and to the right at 45 degrees, as in this figure. The original circle is in green, the first square is in red, and we’re building the blue square above it. The line we just made is dashed. Find the point of intersection between this line and the circle. That point, along with the starting point of the line, defines our first square. Put that at the head of a list. Along with the square’s center x, y and radius, also store two booleans, which I call usedUL and usedLR. Set both to false.

Now comes the iterative algorithm. Scan the list of existing squares for the biggest o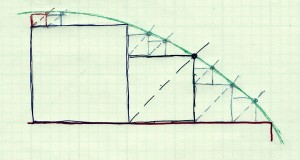ne (that is, the one with the largest radius) for which either usedUL or usedLR are false. Let’s call this square S. If S.usedUL is false, create a 45-degree line up and to the right, starting at the upper-left corner of S. Find the point of intersection of this line with the circle, and that point along with the starting point makes a new square. Add the new square to your list (with both flags set to false), and set S.usedUL for this square to true. If S.usedLR is false, build a 45-degree line going up and right from the lower-right corner of the square, and add that new square to the list as well. Then scan the list again for the biggest square that hasn’t been built on. Just keep repeating this until you want to stop (typically either when you have more than a given number of squares, or the largest one has too small a radius. In my graphics programs, I usually stop when the radius is less than 1 pixel).

A subtlety: you might not want to add tiny squares, like those with a radius less than a pixel. So when you go to add a square to the list, check its radius, and just don’t add it to the list if it’s too small. But remember to still set the parent square’s corresponding boolean to true, though, so you don’t go into an infinite loop of building and ignoring the tiny square!

You get the other octants by symmetry, but you can compute them by adding a few more booleans to each square, and sending out lines to the upper-left, lower-left, and lower-right.

Variations:  If speed is an issue, consider writing a special-case routine that takes just two arguments, the starting point and the circle’s radius, and returns the intersection of a line going northeast from that point with a circle of that radius centered at the origin. Then you can replace a few calculations with constants and save some time

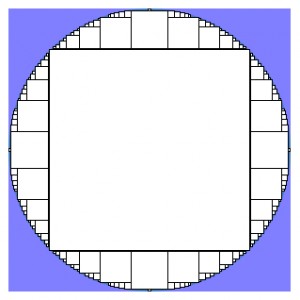If you write a special little loop to seed squares vertically above the first one, then you can make your second-largest squares straddle the midpoints of the biggest square’s edges (hint: use lines that start at each square’s top edge midpoint, and are directed 22.5 degrees clockwise of vertically up). This is probably the version you want most of the time, but the implementation described above is a little simpler since it only uses lines going northeast.

For fun, try extending this algorithm to pack any radial function, not just circles. Hint: sometimes the other two corners of a newly-constructed square will fall outside your function, if it’s curvy enough. You can ignore that, or devise a way to shrink the square so that it fits.