The modulo operator % is great when everything is positive. But when your input value goes negative, the values it returns can be a big surprise.

For example, suppose you have a car going around a 3-mile racetrack. The position of the car is computed by some complicated program, but you get back a floating-point value I’ll call a that tells you how many miles the car has driven after passing the starting line. Because the car can take some warm-up laps before the race begins, you can also have negative values of a, meaning that you have that much distance to travel before the race begins. But the car is still always on the track, so you still need to turn both positive and negative values of a into positions on the track between 0 and 3.

When a>0, then a % 3 is always a number between 0 and 3, and our work is done. But if a is negative, watch out! The result of -1 % 3 is -1. And -4 % 3 is also -1. And -5 % 3 is -2. Though making modulo work this way gives it some nice formal properties, these results can be a real hassle in practice. Here’s how to fix things up.

My solution is to explicitly write some code to give me what I wish modulo did. Here’s a little routine called wrap() that does just that. Instead of calling a % b, you call wrap(a, b). You don’t need to type this in, since it’s already implemented for you in my AU Library. Just make sure you’re including the library, and call AULib.wrap().

// v is input value, m is modulus. wrap(a, b) is a replacement for a % b.
float wrap(float v, float m) {   
  if (m > 0) {
    if (v < 0) v = m-((-v) % m);          // get negative v into region [0, m)
  } else {
    m = -m;                               // the positive value is easier to work with
    if (v < 0) v += m * (1 + int(-v/m)); // add m enough times so v > 0
    v =  m - (v % m);                     // get v % m, then flip the curve negative
  }
  return v % m;                           // return v % m, now that both are positive
}

In practice, wrap() almost always gives me what I wish I got from modulo, even when either or both inputs are negative.

A great example of a place to use wrap() is when you’re using a curve to interpolate data. Suppose you’re using a curve to control the hue of some color. Hue is cyclic around the color wheel in the range [0, 255]. So a hue of 256 should become 0, and 257 should become 1, and so on. That’s hueValue % 255. Modulo! But if you’re using a curve to interpolate your hue values, that curve could dip below 0, giving you negative values for hue. In Processing (and many other systems) negative color values clamp to 0. But we want ours to wrap around, so -1 becomes 255, -2 becomes 254, and so on. Writing hueValue % 255 does not do this: -2 % 255 is -2. But writing wrap(hueValue, 255) gives us just what we want.

Let’s see wrap() in pictures so we know just what we’re giving up and what we’re getting.

Here’s a number line. I’ve marked off sections that are b units wide. The dot in the middle is 0. I’m plotting the results of the built-in modulo operator a % b for values of a from a region slightly bigger than (-2b, 2b). So to the left of the dot, a is less than zero, and to the right, it’s larger.

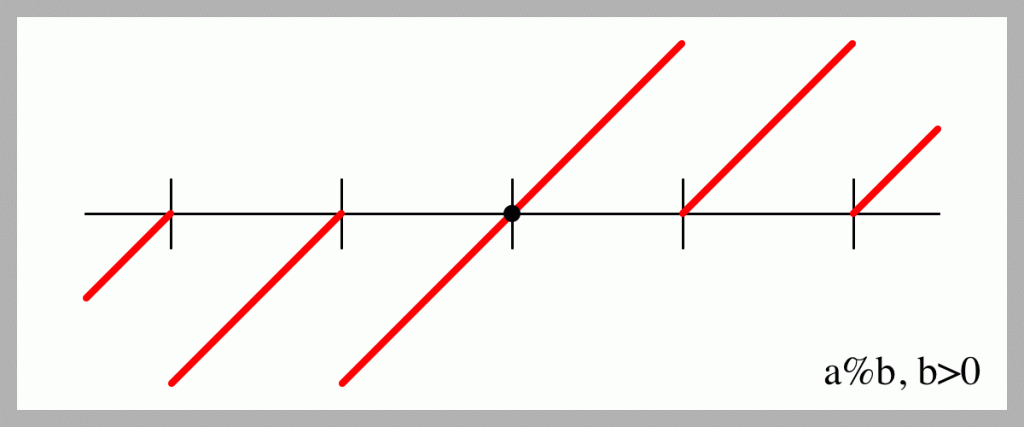
This plot reveals that the result is negative when the input is negative. In almost every program I’ve written, this isn’t what I want, so I have to test for this condition either before or after calling modulo, and manually patch things up. And notice you can’t just make the negative values positive (they’d be sloping the wrong way). You have to do a little computation. And so that you can use this just like modulo, you have to be careful to guarantee that nb % b = 0 for all integer values of n. Here’s a plot of what wrap() returns, which satisfies those conditions and is almost always what I’m after.

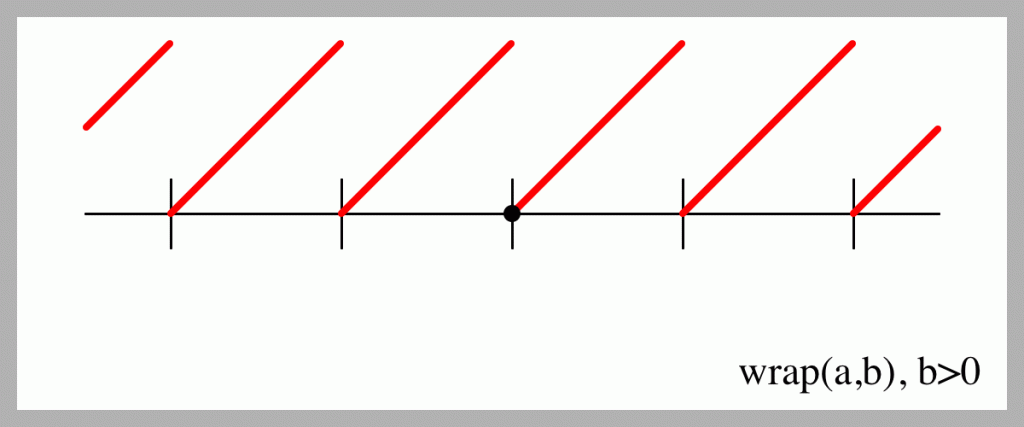
Nice. It’s hard to tell from the picture, but it obeys the condition above: nb % b = 0 for all integers n, even 0. Try printing out a few values if you want to check.

What if the modulus b is less than zero? The next figure shows the built-in a % b for the same range of a, but a negative value of b.

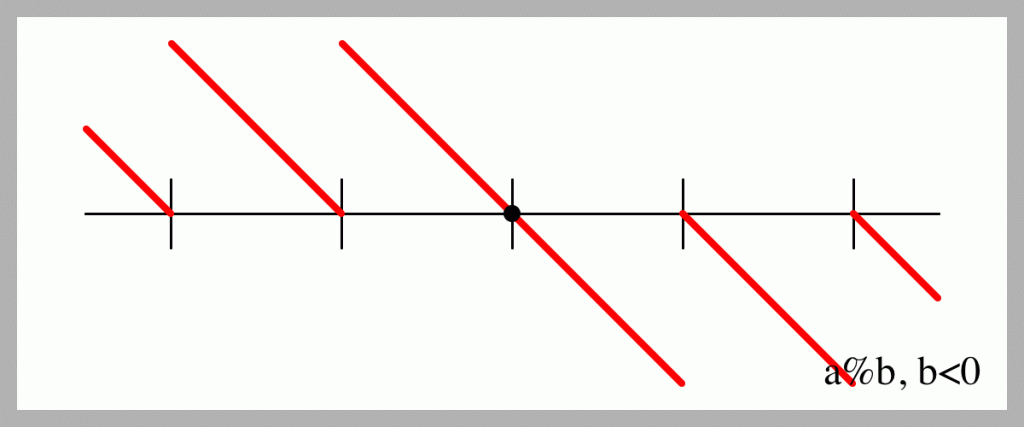
Again, sometimes it’s positive, sometimes it’s negative. But that’s not what really bothers me here: it’s that the line slopes the wrong way in the region [0, b). Think of it this way. When b is positive, then values of a between 0 and b come out of a % b unchanged. In practice, I want the same thing to happen when b is negative: values of a between 0 and b (now negative) should also come out unchanged. This result shows that modulo doesn’t do that.

So let’s make that happen. Here’s what wrap() returns with a negative b. Again, this is almost always what I want in those rare times when b<0.

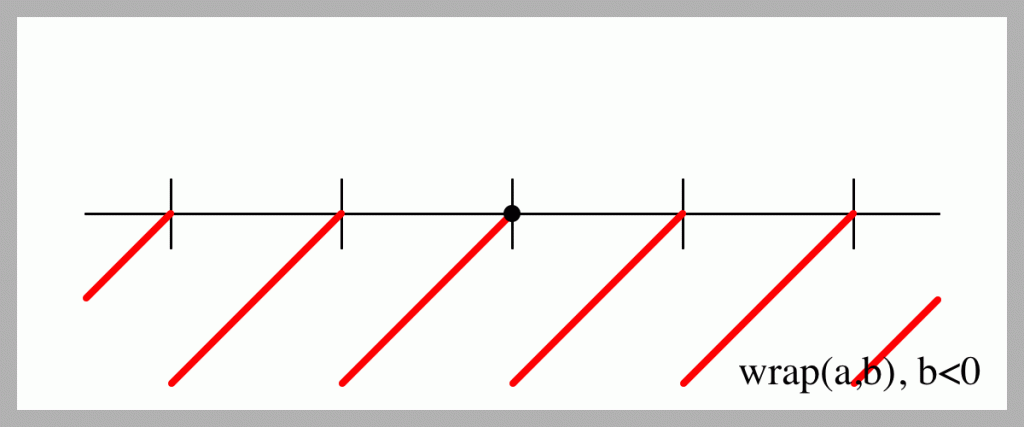
The value of wrap() is that it returns exactly a % b when both values are positive, and it always does what I find to be the most useful thing in all the other cases.

Note: There’s an easier way! Morgan McGuire has a simpler formula that produces the same results as my routine above:

float wrap(float x, float hi) {
  return x - Math.floor(x / hi) * hi
}

This is a shorter and more elegant solution.