Now that my AU Library is out (in beta, anyway) I thought I’d show how to write the noise blending code from an earlier post, but this time using the AU Library. Although I do a little more work in setup(), the draw() is much simpler, and the results are much nicer. Continue reading →

Huzzah! After a seemingly endless gestation period, my Processing library is ready for its beta release!

You can download the file here. Install it into your Processing setup in the usual way (that is, unzip the file and place the results into the libraries folder of your Processing installation. You can find lots of walkthroughs for this procedure online; a nice one can be found here.

The AU library (AU stands for “Andrew’s Utilities”) contains 12 distinct sections, each intended to help you write shorter, cleaner, and more bug-free programs. The sections range from very simple (a single routine to flip a coin) to very powerful (generating equally-spaced points on multi-segment curves). The library is thoroughly documented with motivation, explanations, lots of pictures, and lots of complete examples with source code.

This beta release is meant to be a shakedown cruise. I’d love to have lots of people use this and help me make it even better before I formally release it.

Follow the break for a summary of the library’s contents. Continue reading →

In my AU library, I offer some utilities related to curves. Although Processing offers functions for finding points on curves, I needed to write my own implementation that was fast and efficient. Here’s an easy, elegant way to compute points on Catmull-Rom and Bezier curves, along with a discussion of an idea for making it faster. Continue reading →

Some people have asked for an implementation of the noise blending technique in my previous post. Here’s the Processing code for the core idea. Keep in mind that this is just about making a smoothly changing noise field; what you do with that noise is up to you! Continue reading →

We often use Perlin-esque noise functions to create complex graphics (the noise function built into Processing is just such as function). We can save a value of noise at every pixel in our graphics window, creating a field of noise. The value of these fields is that, unlike white noise, these fields contain visible structure at multiple scales, and that structure usually creates interesting graphics. But when we animate these images they often seem to be missing a certain oomph. This note discusses one way to get that excitement back in there! Continue reading →

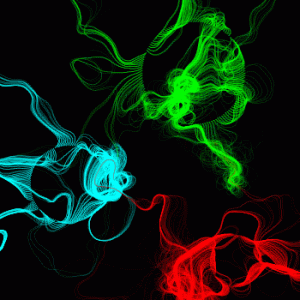I’ve been making little doodles with my new Processing library. The goal is to make it better by finding and fixing bugs, and making it easier to use overall. Here’s something I made this morning roughly based on an earlier sketch. It uses my 2D array to store multiple noise images, my animation controller to sequence the noise fields, and my camera to make motion-blurred final frames. Click the picture to see the animation!

While programming in Processing, I’ve developed about a dozen useful tools for everyday work. I’ve packaged these up in a library which I call AU, for “Andrew’s Utilities.” I’ll be sharing it as soon as I finish the documentation. Although the official Processing wiki has a nice walkthrough for how to make a library, there are a few things that I spent considerable time figuring out. Here’s what I learned, to save you the effort.
Continue reading →

Here are the slides for a talk I gave at SIGGRAPH 2014 in Vancouver, B.C., The talk was about my experiences putting together the Imaginary Institute class, “2D Animation and Interaction.” You can download the slides here.

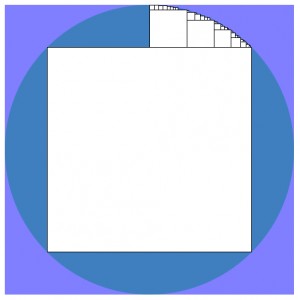
Here’s a fun algorithm: put the biggest possible square into a circle. Then looking at just the right side of the space above that square, add in the biggest possible square, then add in the biggest square into the space that remains, and so on, filling up that octant of the circle. It’s not too hard. My solution’s after the break. Continue reading →

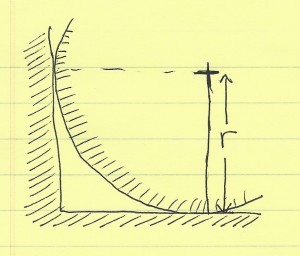Given a circle of radius r, and around it a box of side 2r. We want to put another circle into the gap between the circle and a corner of the box. Find a formula for the center and radius of the largest circle that can be fit into that space. This might be a little trickier than you first think.

The solution’s after the break, but don’t give up too soon!  Continue reading →