The AU Library:
Measuring Distances

Andrew Glassner
https://The Imaginary Institute
15 October 2014

andrew@imaginary-institute.com
https://www.imaginary-institute.com
http://www.glassner.com
@AndrewGlassner

Imaginary Institute Tech Note #6

Table of Contents

• Introduction
• Types of Distances
• Radial Distance
• Linear Distance
• Box Distance
• Plus Distance
• Angle Distance
• N-sided Polygon Distance
• N-pointed Star
• Tech Talk
• Resources

Introduction

When we create images and animation, we often want to know the distance between two things. Often these are two points on the screen, which might represent the centers or edges of two objects. But sometimes we want to find a distance in time, or even in color.

In this note I will show you how to measure distances in several different ways, using my AU (Andrews Utilities) library. For simplicity, I'll restrict the discussion to measuring the distance between 2D points on the screen, but remember that you can use these tools to measure any kind of distance.

The distance were all familiar with is the Euclidean straight-line distance. We draw a straight line from one point to the other, and the length of that line is the distance between them. That's a great definition for distance and its served us very well for centuries.

But its not the only game in town. An entire branch of mathematics has developed specifically for talking about different kinds of distance. Mathematicians call a way of measuring distance a metric. So though the Euclidean straight line is probably the best known and most-used metric, we can imagine and use others.

In this library I offer 7 different metrics for measuring distance. Five of them use one function call, while two others use another call that takes just one more argument. This makes it easy to just swap out one metric for another in your sketch, and see if things become cooler, or at least more interesting.

One issue that always crops up with the traditional Euclidean distance is that it leads to complications when we change the size of our sketch window. For example, suppose you're drawing an animation loosely based on gravity: the closer two objects are to one another, the more each each tries to move towards the other. You prototype your sketch on a window that's 500 by 500 pixels, and you tune everything up so that when two objects are on opposite sides of the screen they ignore one another, but when the're both near the middle they come together. You set thresholds of 400 and 100 pixels to set where these two effects occur.

Now you decide to make your window 900 by 900 pixels. You want things to look the same, just on a bigger scale. But your program is locked into the numbers 400 and 100 you hand-tuned, because those were the distances that looked good. Those numbers now have to change. In this example that wouldn't be too hard, since you could just scale your two numbers by 900/500, but in other cases it can get pretty messy.

In this library, I take a different approach. The routine takes arguments giving it the locations of 2D points A and P, and it returns some kind of distance between them. But it also takes a third, helper point B. Point B defines the geometry of the situation, and the length from A to B (or to a point derived from B) has length 1.

For example, in my version of the straight-line metric, the point B provides us with a single point on a circle around A. The distance from A to B is the radius of that circle. our distance is given by the straight-line distance from A to P divided by the straight-line distance from A to B, as shown here.

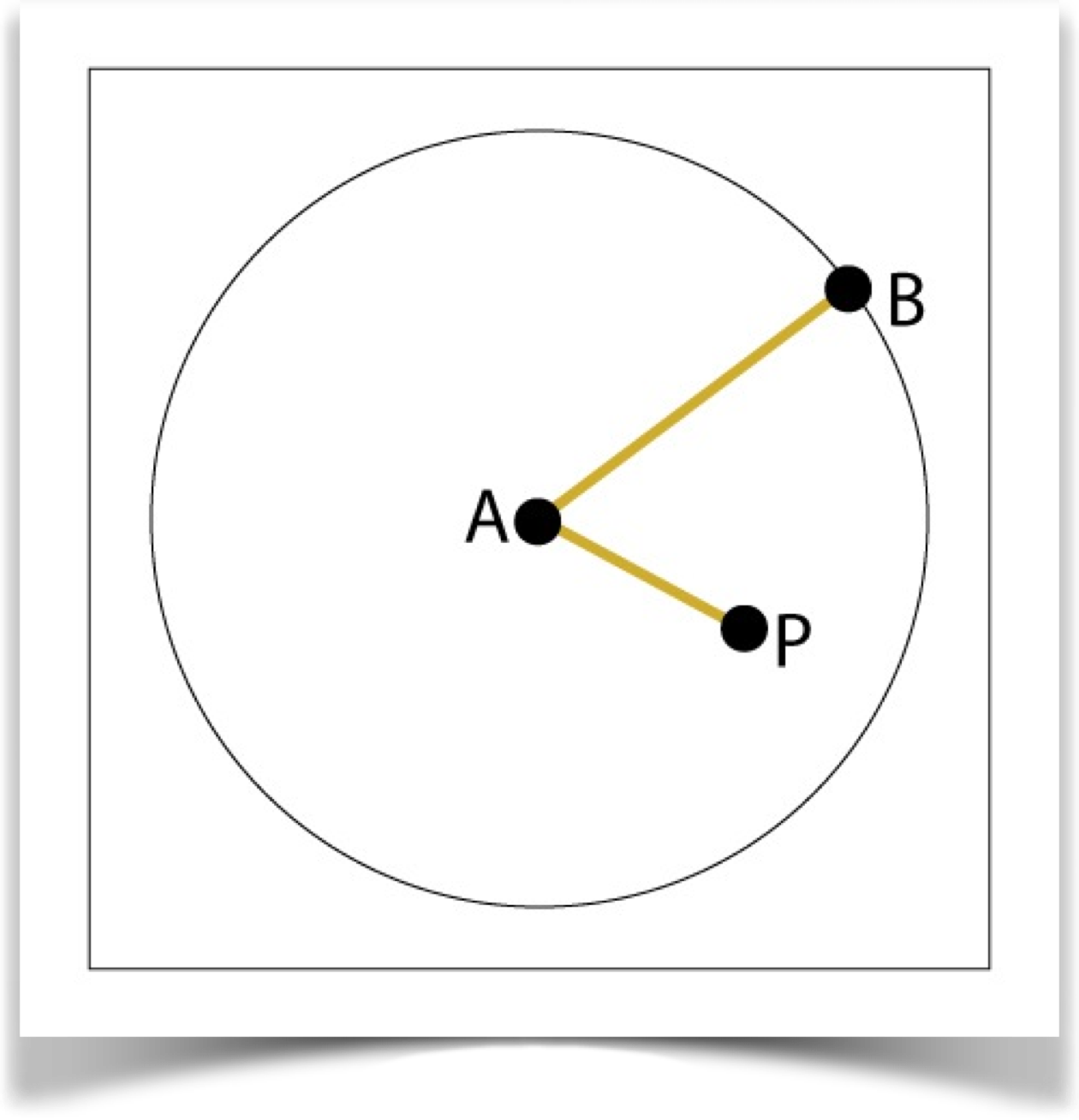
So points P that are closer than B return a distance between 0 and 1, and those farther than B return a value greater than 1. Points P on the circle have a distance of 1.

With this scheme, you don't have to worry about the size of your graphics window. As long as your points are always proportionally in the same place, you'll always get back the same measurement of distance.

Types of Distances

Recall that we measure the distance between A and P, using B as a helper.

To find distances, most of the time you only need to call one function:

float dist(int distanceType, float ax, float ay, 
	                         float bx, float by, 
	                         float px, float py);

Here are your choices for distanceType, all discussed in detail below:

• DIST_RADIAL
• DIST_LINEAR
• DIST_BOX
• DIST_PLUS
• DIST_ANGLE

When you call dist(), remember to precede both the function and your choice of distanceType with AULib.. For example, you might write

float myDistance = AULib.dist(ax, ay, bx, by, px, py, AULib.DIST_BOX);

Were used to distance being either 0 or positive. Two of these options ( DIST_LINEAR and DIST_PLUS ) return a signed distance, in which the distance can be positive or negative. The sign of the distance tells tell us something about the geometry of the point P relative to A and B. If you're not interested in that aspect of things, you can just take the absolute value of the distance (e.g., abs(d)), which will always return a non-negative value.

There is a second function to know about. It just adds one new parameter, n, after the distance type. This gives the function a little more information on the geometry you want it to use:

float distN(int distanceType, int n, float ax, float ay, 
                                     float bx, float by, 
                                     float px, float py);

This function recognizes only two values for distanceType:

• DIST_NGON
• DIST_STAR

These distances generalize two of the ones from the other list. That is, DIST_NGON is a more general DIST_BOX, and DIST_STAR is a more general DIST_PLUS. So the're more flexible, but the're also a little bit slower. Well see more about them below.

Remember not to mix up the difference values of distanceType. These last two values should only be used with distN(), and the others should only be used with dist().

A note on terminology. The Euclidean straight-line distance between points A and B is traditionally written |AB|, and I'll do that here. By contrast, the distance measured by the metrics in this library will be written <A+B>.

For example, the distance returned by the straight-line metric in this library, as discussed above, is given by <AP> = |AP|/|AB|. In words, our straight-line distance from A to P is the Euclidean distance from A to P divided by the Euclidean distance from A to B.

In general, if points A and B are identical, you'll get back a distance of 0. When points are farther away from A than the distance to B, their distance is greater than 1. The farther they get, the greater this distance gets. So there is no maximum value on these functions (though if you use them for screen distances, the diagonal of the window is a practical upper limit between visible points).

Now well look at each of the metrics and see what they offer us.

Radial Distance

The radial distance is specified with type DIST_RADIAL.

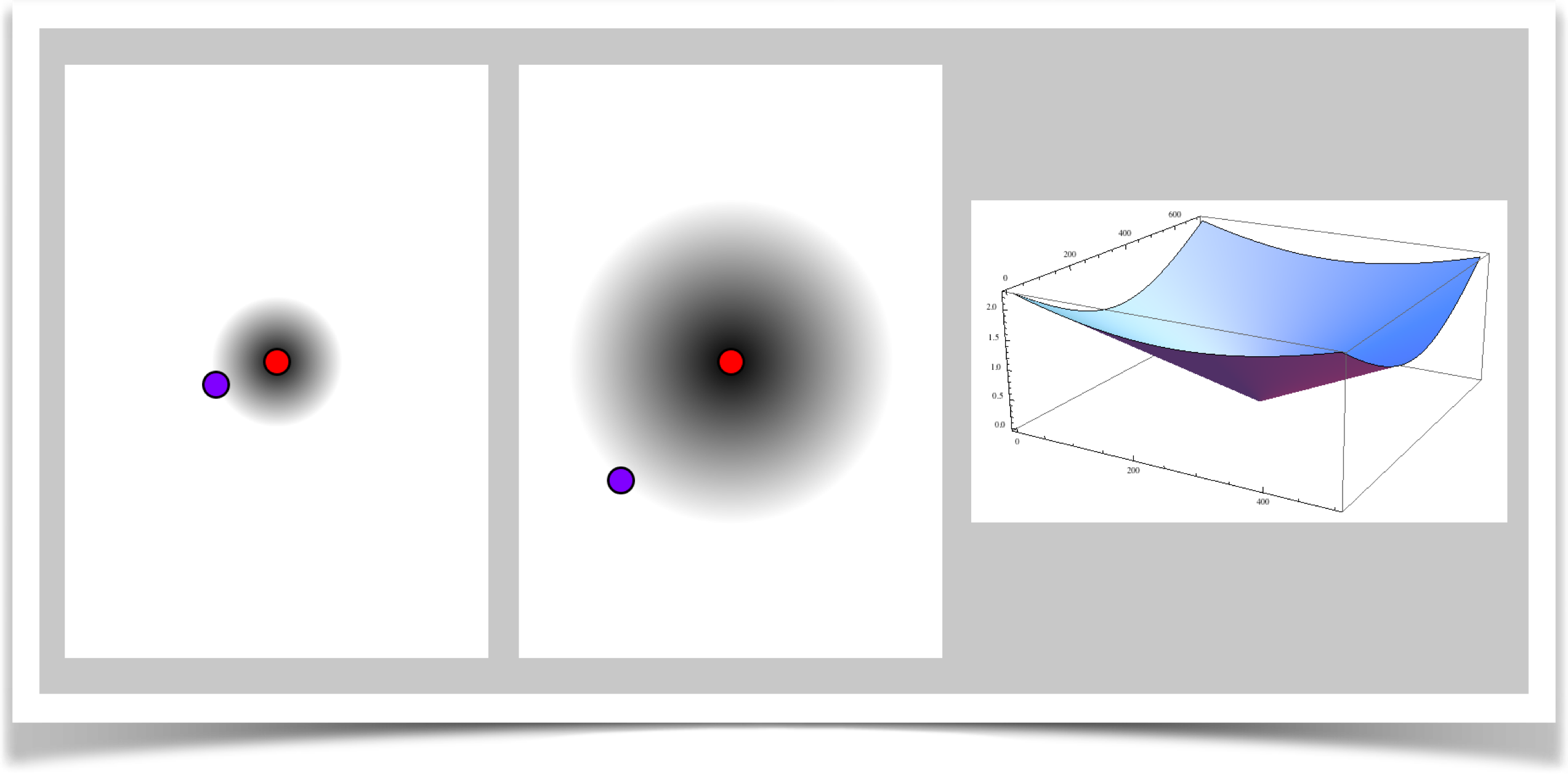
The radial distance is our old friend from Euclidean geometry. But as always, I divide it by the distance from A to B. Thus <AP> = |AP|/|AB|. The figure below shows the geometry. In this figure (and all the others to come), pointA is in red, and point B is in purple. Each point in the grayscale picture shows its distance from A, where 0=black and 1=white. Values below 0 or above 1 are clamped to that range, so its easier to compare the various grayscale pictures.

In this setup, all distances are 0 (if P is the same as A) or positive. The height plot on the right is a piece of a cone, like an ice-cream cone. The farther a point P is from A, the bigger its distance. If P is closer to A than B is, the distance is less than 1. Otherwise, the value is greater than 1.

Linear Distance

The linear distance is specified with type DIST_LINEAR.

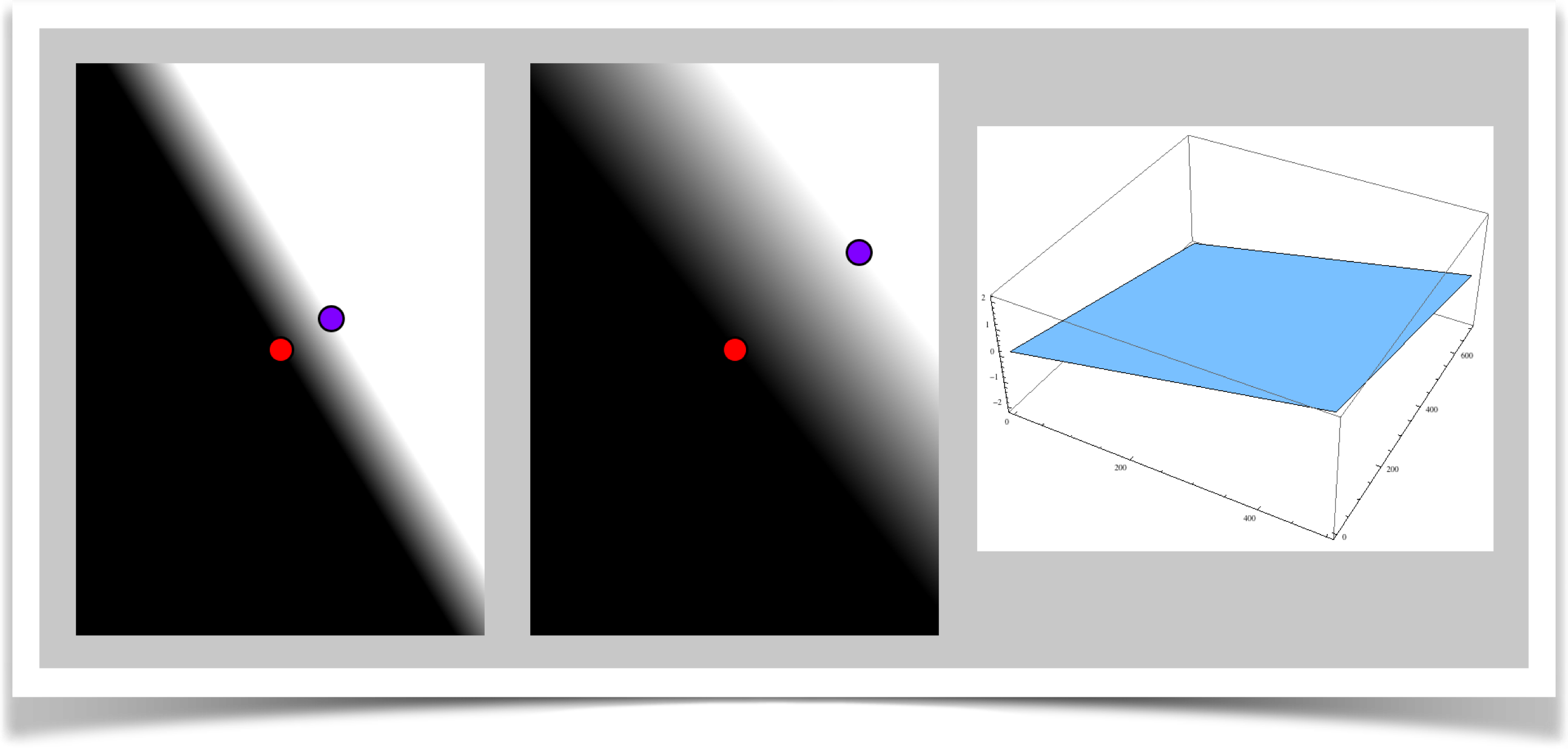
In this metric, points A and B determine a line. We measure the distance from A to P by using just the component of that distance that is parallel to AB.

One way to think about this is that every point P is pushed along a line perpendicular to AB until it hits the line AB. If that new point is between A and B, it has a distance between 0 and 1. If its farther away from A than B, its distance is greater than 1. If its behind A, then its value is negative, and gets increasingly negative as it gets farther from A. If you just want the absolute distance, use the abs() function to throw away any negative values.

Box Distance

The box distance is specified with type DIST_BOX.

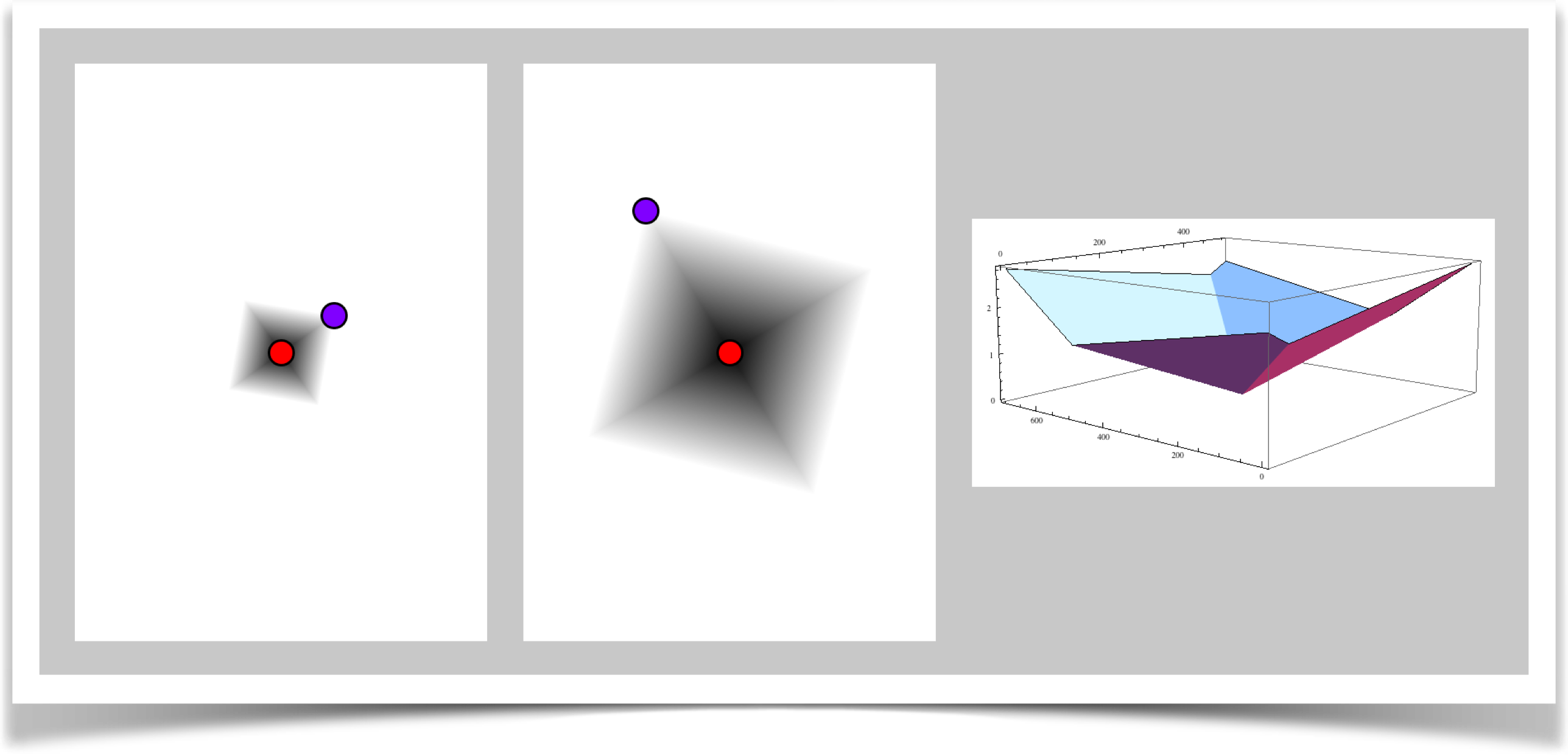
This style is a generalization of a famous measure called the taxicab distance. Imagine that you live in a city where the streets are formed in a square grid. The distance between two points is the distance that must be covered by a taxi that drives between them. A little thought will reveal that if two points are separated by a units in X, and b units in Y, the taxicab distance is a+b.

Here you get to set up the taxicab grid in any angle and size you like. The point A is in the center of a square, while B is at one corner, as shown below.

An interesting wrinkle in this measure is that we don't divide the distance from A to P by the distance from A to B, as in most of the other measures. Rather, we divide it by the distance to the nearest point on the square defined by A and B. That means that everything inside the square has a distance between 0 and 1, points right on the square have a distance of 1, and points outside the square have a distance greater than 1.

In this setup, all distances are 0 (if P is the same as A) or positive.

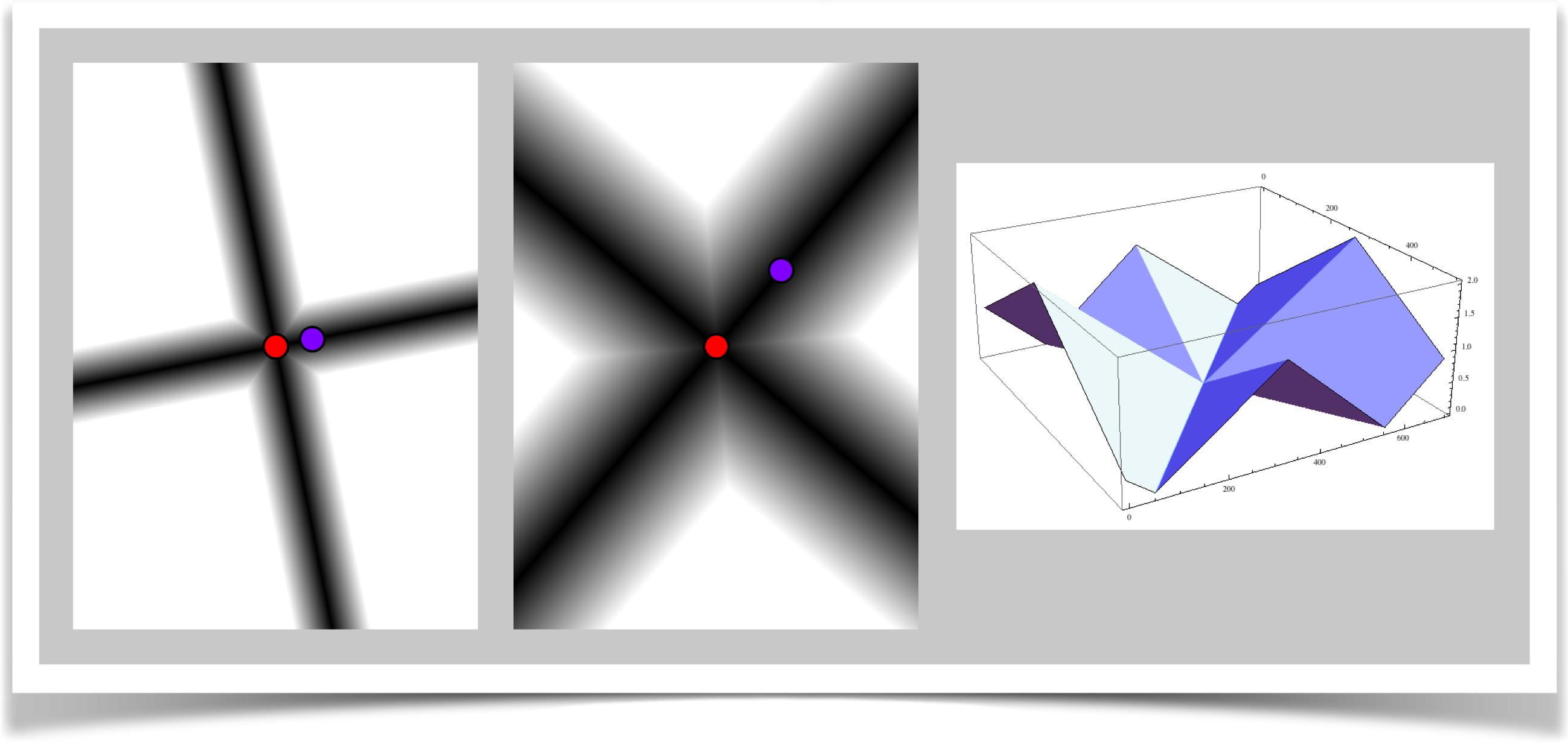
Plus Distance

The plus distance is specified with type DIST_PLUS.

This is just like the linear form, only we use two lines. The first is the line though A and B, and the second is the line perpendicular to that, also through A. The distance returned is the smallest distance to either of these two lines.

In this setup, all distances are 0 (if P is the same as A) or positive.

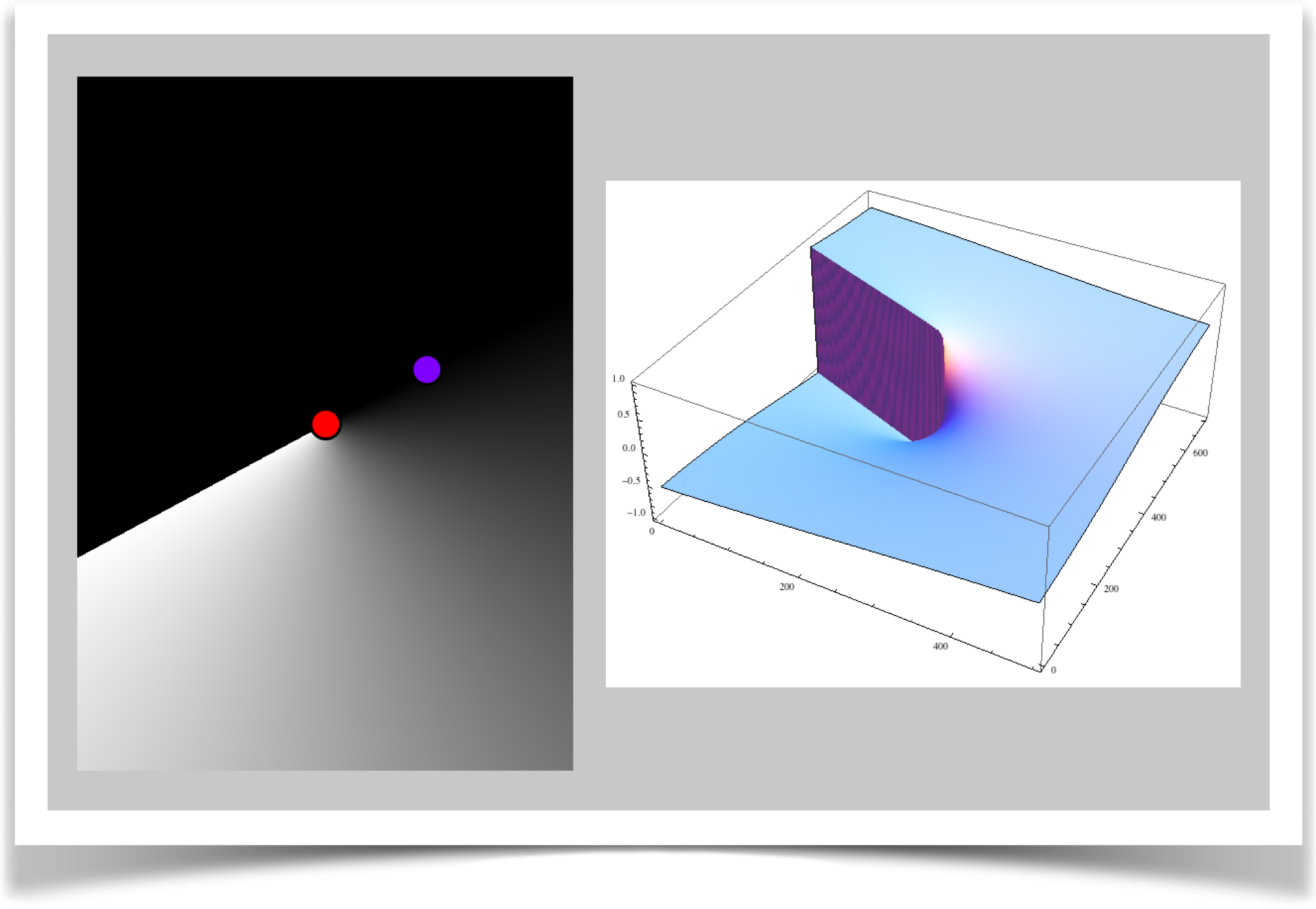
Angle Distance

The angle distance is specified with type DIST_ANGLE.

Here we measure the clockwise angle between the line AB and the line AP. The angle is in the range $[-\pi, \pi]$ radians (that's [-180, 180] degrees), which gets scaled to [-1, 1]. Note that the distance of B from A is irrelevant in this measure, since were only concerned with angles.

Think of this like a clock. Point A is in the middle of the clock, and point B is at the end of the minute hand. Point P, which were measuring, is on the second hand. If P is clockwise of B, but not more than 180 degrees, then we get back the angle divided by 180, so its from 0 to 1. On the other hand, if P is counter-clockwise of B, we get back a value from 0 to -1.

N-sided Polygon Distance

The N-sided polygon distance is specified with type DIST_NGON.

This is the first of the two types that you call with distN() (note the N in there). Its a generalization of DIST_BOX. As we saw, one way to think of DIST_BOX is that it pretends that there's a square around A, with one vertex at B, and it checks the distances from A to P through the midpoint of each edge. DIST_NGON does the same thing, only instead of a box, it uses a polygon of any number of sides. The parameter n tells it how many sides to use for the polygon.

The name of this style comes from the phrase N-sided polygon, often abbreviated as ngon (pronounced en'-gon).

In this setup, like DIST_BOX , all distances are 0 (if P is the same as A) or positive. Here's the grayscale picture. As before, 0 is black, and anything above 1 is white.

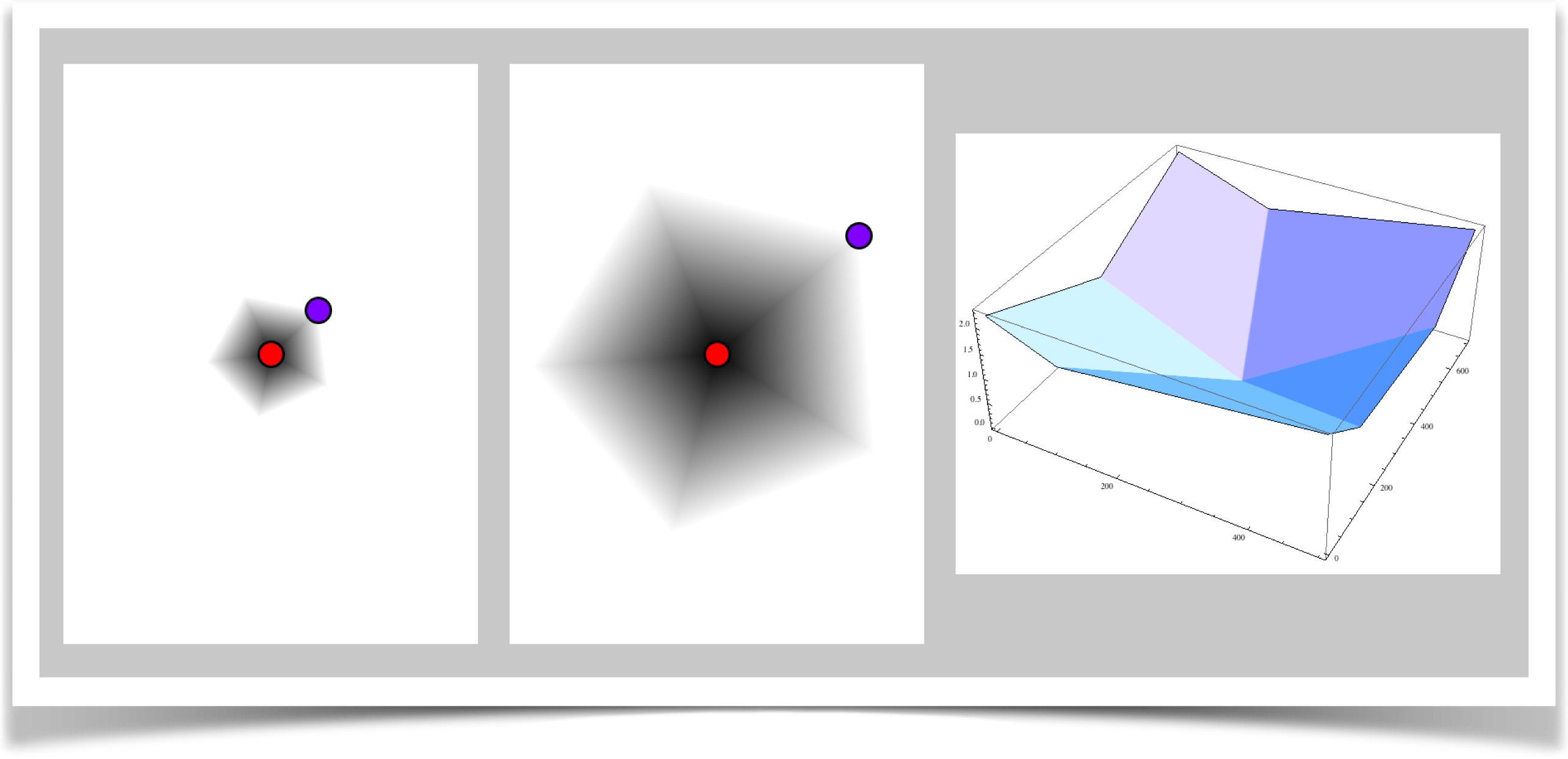
You might notice that DIST_NGON with n=4 will give the same results as DIST_BOX. Why are there both versions? Simple: speed. The box version is quite a bit faster because the geometry of a box let me optimize the code for that special case. Since using the box style is pretty popular, I left it there so your programs can run a little faster for those times when it's a box you want (that is, n=4). Keep in mind that as n grows larger, this routine takes longer (not a lot, but it can add up if you call it many times per frame).

N-pointed Star

The N-pointed star distance is specified with type DIST_STAR.

This is the second of the two types that you call with distN() (again, note the N in there). Its a generalization of DIST_PLUS . Recall that measure finds the line from A through B, and the perpendicular line through A, and finds the distance of P to the nearest point on both lines. It returns the nearer of the two.

This version generalizes that idea. We think of the lines here as radiating from the center point A. Thus the plus sign would have 4 lines. But with this call you can use n lines, and returns to you the nearest distance to any of them.

In this setup, like DIST_PLUS , all distances are 0 (if P is the same as A) or positive.

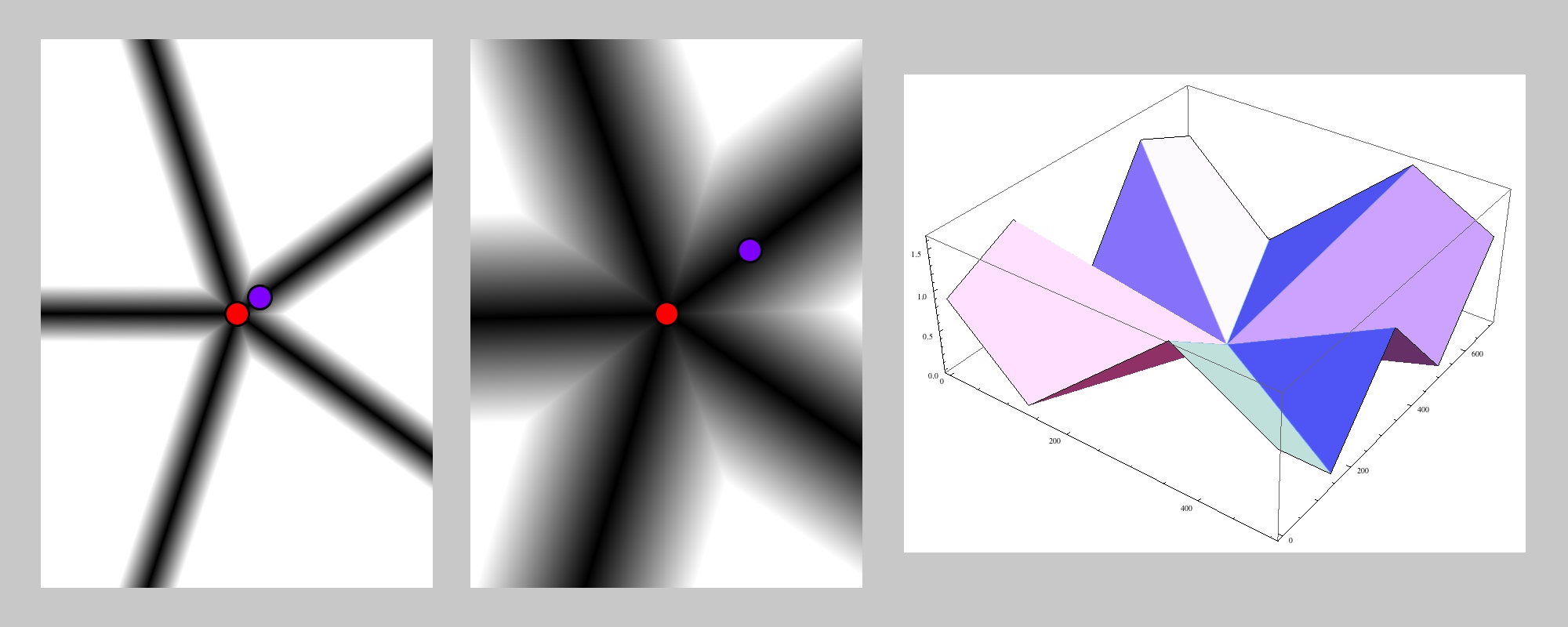
As with the polygon/box measures we just saw, you might notice that DIST_NGON with n=4 will return the same values as DIST_PLUS. The reason for having both versions is the same as before: speed. The plus style is faster, because the geometry of a plus sign let me write fast code for that special case. And that case is pretty handy, so its worth having a faster version around. As with the polygon, keep in mind that as n grows larger, the routine takes longer (not a lot, but it can add up if you call it many times per frame).

Tech Talk

Here are some details on the distances provided by the library. None of this is necessary for using the library, so you can skip this section if you're not into the math and programming side of things.

The distance metrics are just some basic vector algebra and trig. I'll go through the geometry here briefly, but I won't go into every detail (you can always look at the code and follow it step by step).

Radial

Find distances |AB| and |AP|. Return the distance <AP> = |AP|/|AB|.

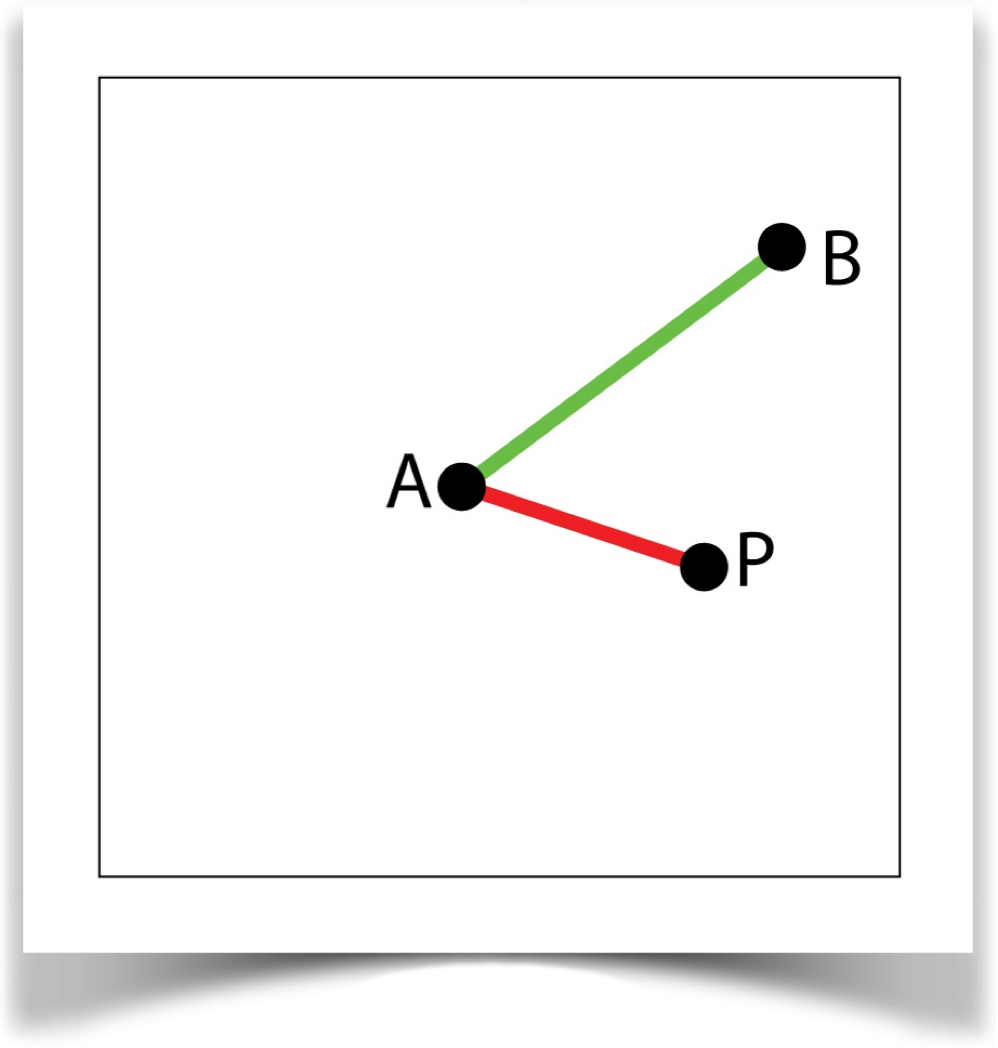
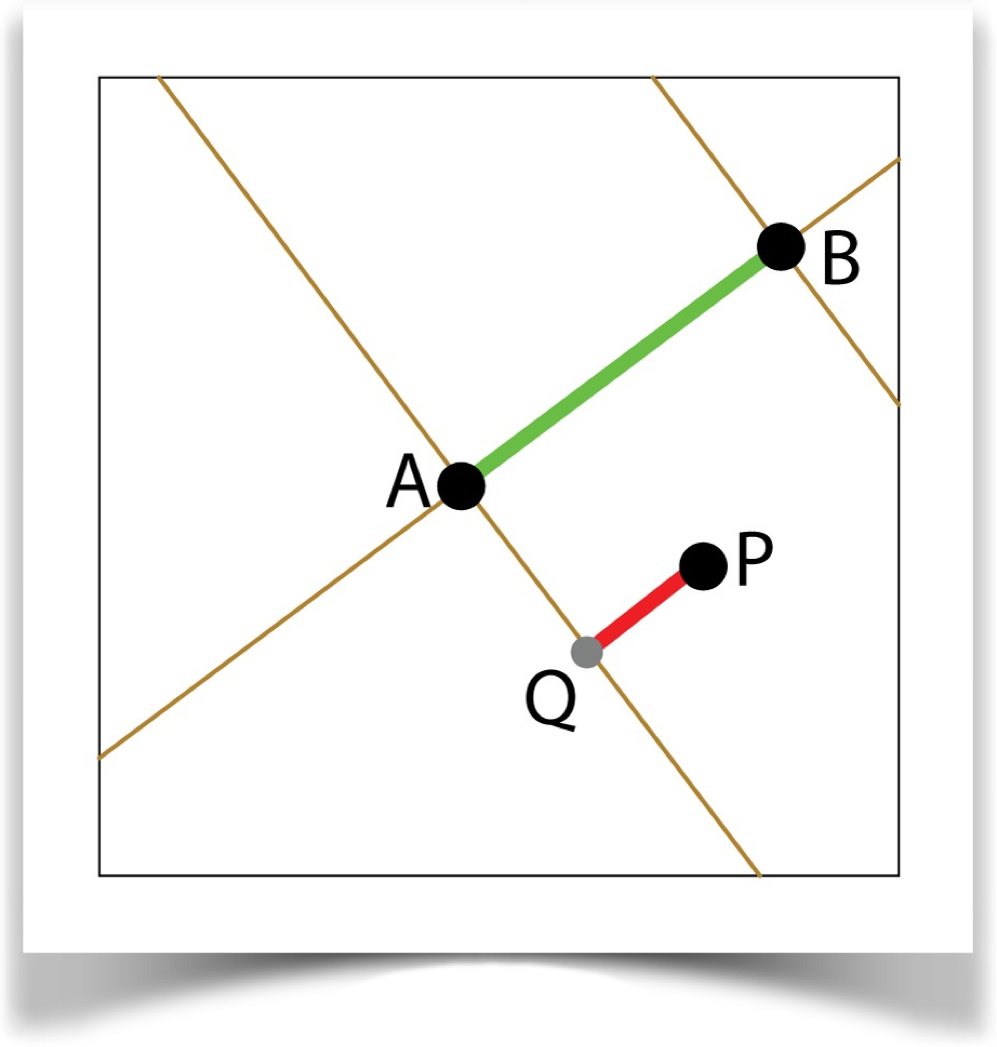
Linear

From line AB, construct a perpendicular through A. Find the nearest point on this line to the point P, and call this point Q. The distance is <AP> = |PQ|/|AB|.

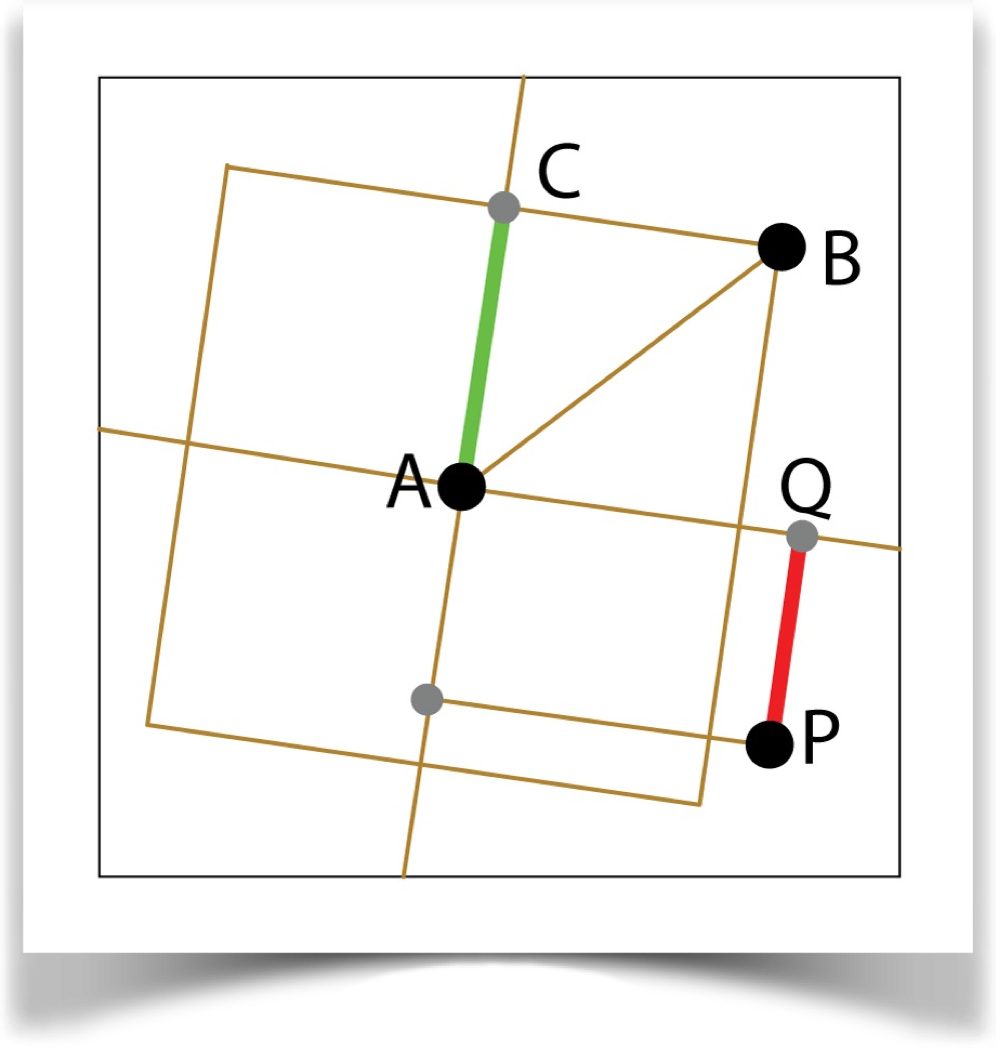
Box

Find point C, the midpoint of a side of a square centered on A with a corner at B. Construct a line AC and a line perpendicular to AC through A. Find the nearest point on each of these lines to point P. Select the point nearest to P, call it Q. Return the distance <AP> = |PQ|/|AC|.

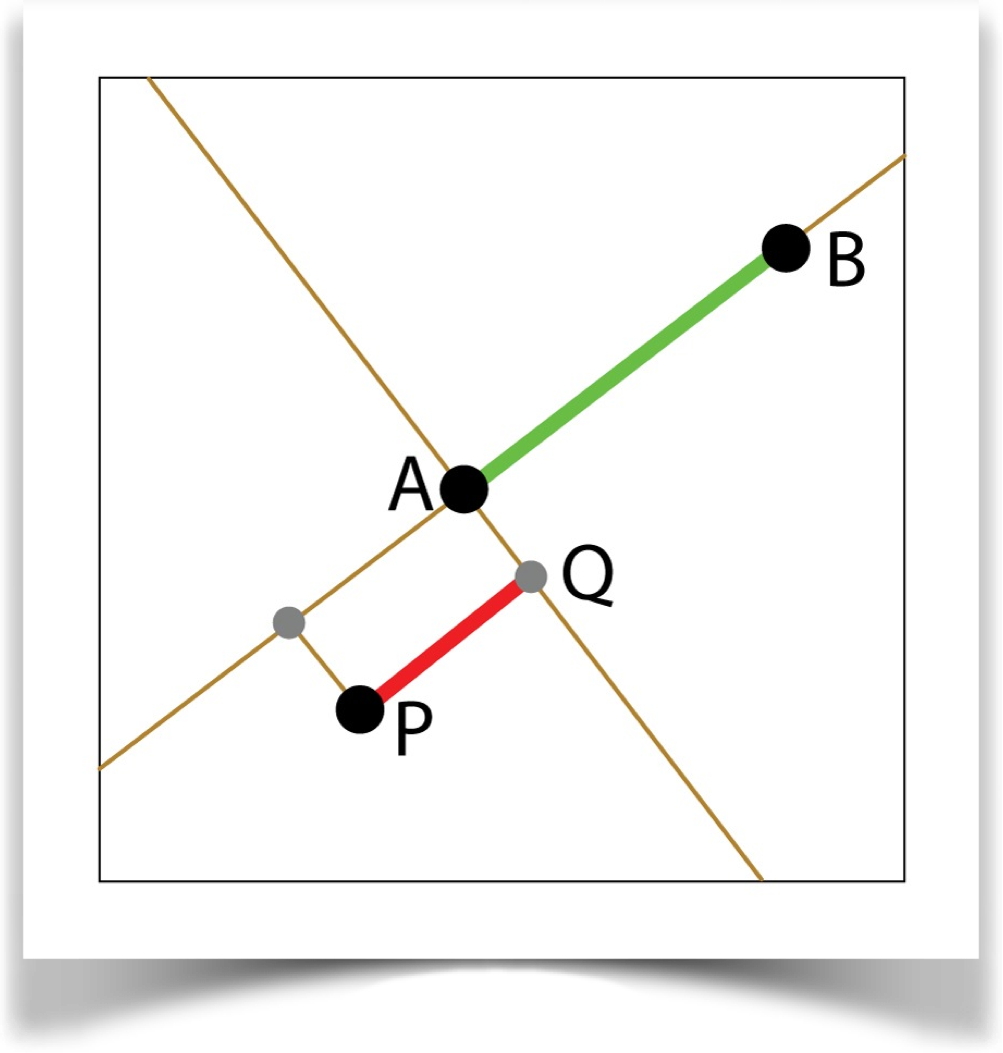
Plus

Construct the line AB, and a line perpendicular to AB through A. Find the point on each of these lines closes to P. From these, select the one closest to A and call it Q. The distance is <AP>=|PQ|/|AB|.

Angle

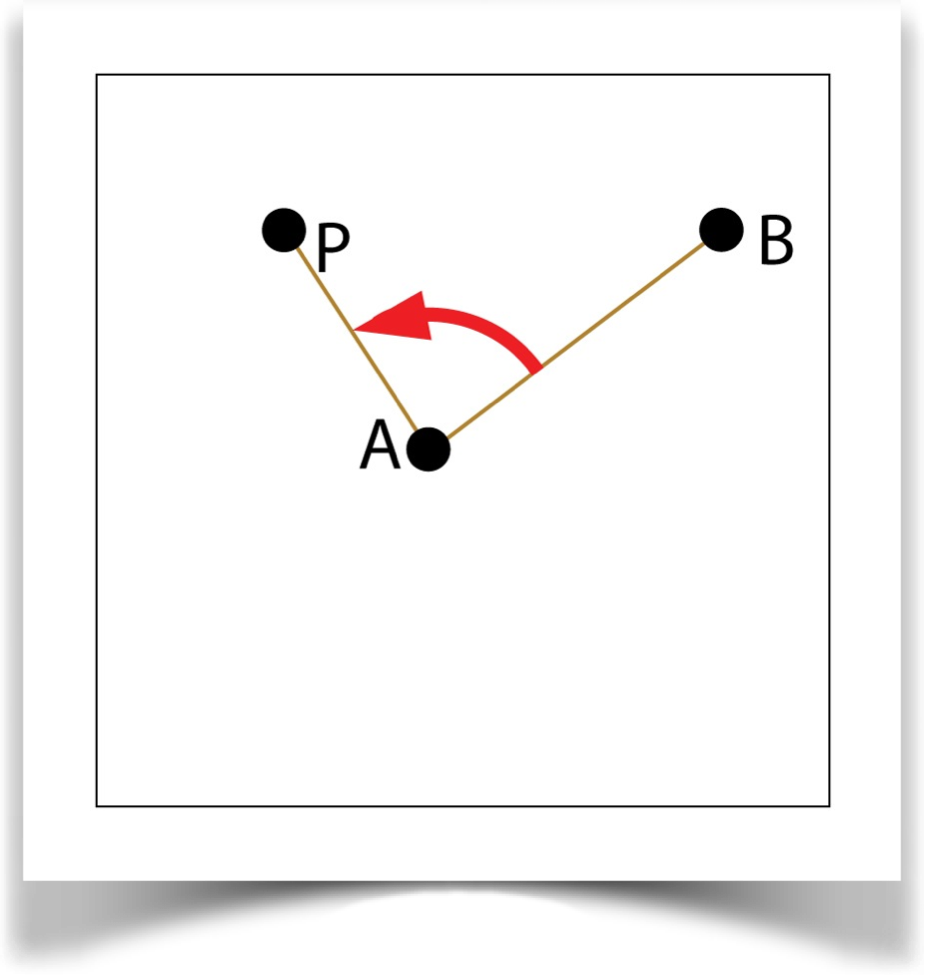
Find the angles (measured clockwise, with the positive X axis as 0) of lines AB and AP. Find their difference and divide by . If P is counter-clockwise from B, make it negative.

Ngon

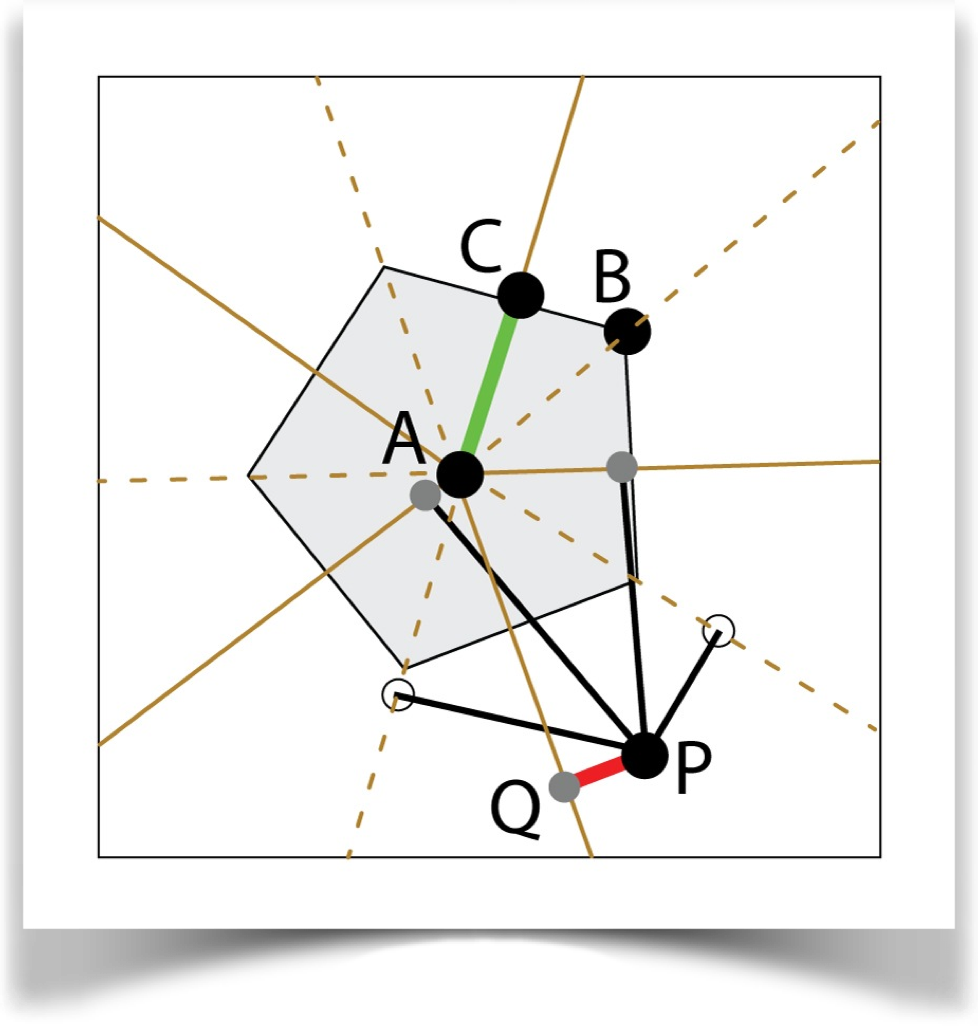
Construct an n-sided polygon centered at A with one vertex at B. Find C, the midpoint of any edge. Construct lines from A through the midpoint of each edge, and find the closest point on each such line to P. From the points that are on the half-lines from A through an edge (solid in the figure), choose the one closest to P and call it Q. Using these points, return <AP> = |PQ|/|AC|.

Star

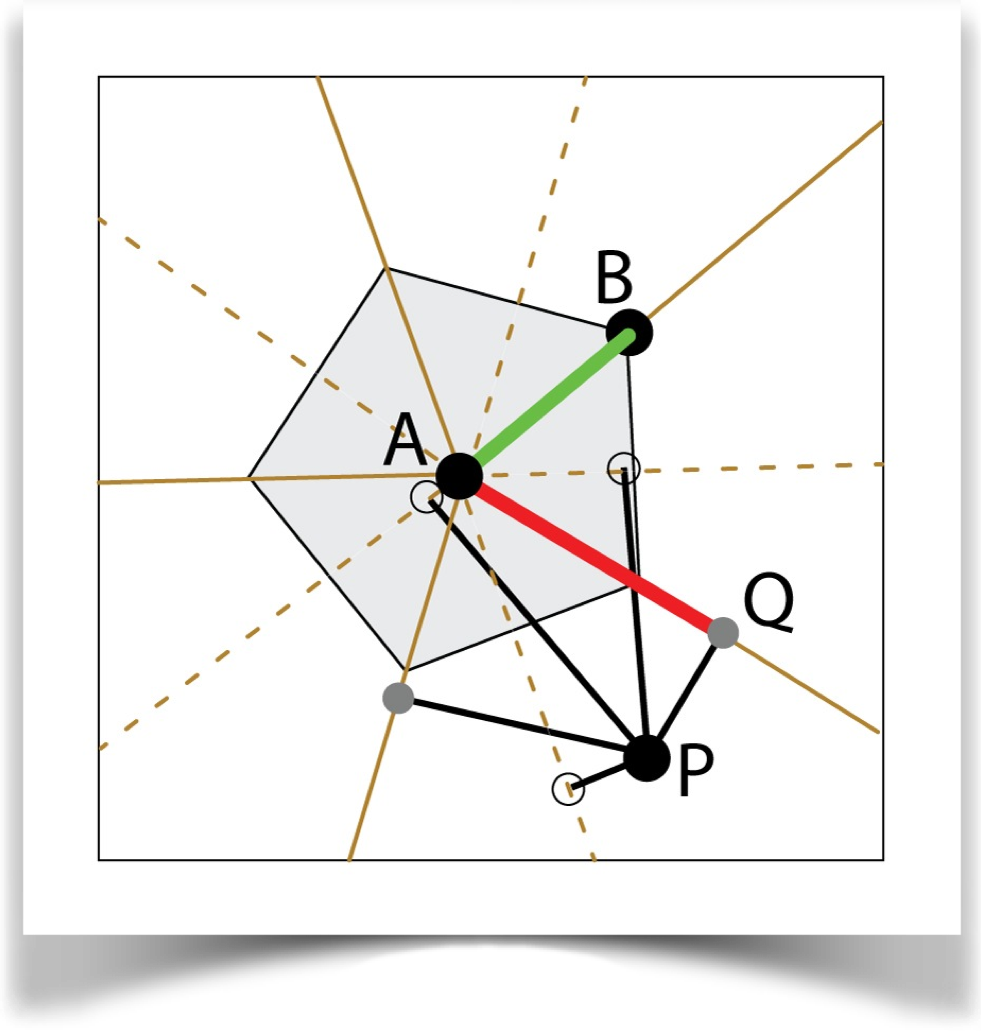
Construct an n-sided polygon centered at A with one vertex at B. Construct lines from A through each vertex. Find the closest point on each such line to P. From the points that are on the half-lines through A and a vertex (solid in the figure), choose the point closest to P and call it Q. Return |AQ|/|AB|.

Resources

The library, examples, documentation, and download links are all at the Imaginary Institutes resources page:

https://www.imaginary-institute.com/resources.php

To use it in a sketch, remember to include the library in your program by putting

import AULib.*;

at the top of your code. You can put it there by choosing Sketch>Import Library... and then choosing Andrew's Utilities, or you can type it yourself.

This document describes only section of the AU library, which offers many other features. For an overview of the entire library, see Imaginary Institute Technical Note 3, The AU Library.