Wrap: A Practical Replacement for Modulo

Andrew Glassner
http://The Imaginary Institute
Version 1.0: 13 July 2015

andrew@imaginary-institute.com
http://www.imaginary-institute.com
http://www.glassner.com
@AndrewGlassner

Imaginary Institute Tech Note #12

Abstract

The standard modulo operator is great when both inputs are positive. But when one or both inputs are negative, the results are almost never useful from a programmer's perspective. I present a routine wrap(a, b) that produces the same result as modulo when both inputs are positive, but returns results more useful for programmers in all other cases.

The Problem With Modulo

The modulo operator, usually written a%b, can produce surprising results when either or both inputs are negative.

For example, suppose you have a car going around a 3-mile racetrack. The position of the car is computed by some complicated program that gives you a floating-point value that I'll call $a$. This tells you how many miles the car has driven after passing the starting line at the start of the race. Because the car can take some warm-up laps before the race begins, you can also get back negative values of $a$, meaning that you have that much distance to travel before the race begins. But the car is still always on the track, so to figure out where to draw it you still need to turn both positive and negative values of $a$ into positions on the track between 0 and 3.

When $a>0$, then a%3 is always a number between 0 and 3, and our work is done. But if $a$ is negative, watch out! The result of $-1 \% 3$ is $-1$. And $-4 \% 3$ is also $-1$. And $-5 \% 3$ is $-2$. This means we'd have to do extra work to fix these values before handing them to our car-drawing routine, which is expecting a value from 0 to 3.

Though making modulo return negative numbers in these circumstances gives it some nice formal properties, these results can be a real hassle in practice.

Note that languages differ in their definition of what modulo returns in the presence of one or more negative inputs (see this Wikipedia article). Many popular languages, like various flavors of C, Javascript, Python, and Ruby, can return negative values as a result of modulo, which is the problem I'm addressing here. For the examples and discussion in this note, I'm using the implementation in Java 8 for the Mac.

A Pragmatic Replacement for Modulo

My solution to this problem is to explicitly write some code to give me what I wish modulo did. Here's a little routine called wrap() that does just that. Instead of calling a%b, you call wrap(a,b). There are a million ways to code this; here's a version that I feel is fast but not too cryptic.

// v is input value, m is modulus. wrap(a, b) is a replacement for a % b.
float wrap(float v, float m) {   
  if (m > 0) {
    if (v < 0) v = m-((-v) % m);          // get negative v into region [0, m)
  } else {
    m = -m;                               // the positive value is easier to work with
    if (v < 0) v += m * (1 + int(-v/m));  // add m enough times so v > 0
    v =  m - (v % m);                     // get v % m, then flip 
  }
  return v % m;                           // return v % m, now that both are positive
}

In practice, wrap() almost always gives me what I wish I got from modulo, even when either or both inputs are negative.

Another nice feature of wrap() is that it reduces the mayhem caused by the various definitions of modulo in different prorgramming languages. Using wrap(), you always know what you'll get, no matter what language you're using (though of course wrap() would need an implementation in your language of choice).

You might notice that wrap() uses modulo! If you follow things through, you'll see the modulo operator is only used when both of its inputs are known to be positive.

Using wrap()

A great example of a place to use wrap() is when you're using a curve to interpolate data. Suppose you're using a curve to control the hue of some color. Hue, when used as part of the HSL or HSB color systems, is cyclic around the color wheel. Let's say it's in the range [0, 255]. So a hue of 256 should become 0, and 257 should become 1, and so on. Writing hueValue for our hue variable, we could just write hueValue%255 to get what we need. Hooray for modulo!

But if you're using a curve to interpolate your hue values, that curve could dip below 0, so that hueValue would be negative. In Processing (and many other systems) negative color values clamp to 0. But we want ours to wrap around, so -1 becomes 255, -2 becomes 254, and so on. Writing hueValue%255 does not do this: -2%255 is -2, not 254. But wrap(hueValue, 255) is 254, which is what we want.

Comparison of Modulo and wrap()

Let's see wrap() in pictures so we know just what we're giving up and what we're getting.

Here's a number line. The horizontal axis is $a$, our first argument to wrap(). The vertical axis is the result of either modulo or wrap(a,b), with positive Y going up the page. I've marked off sections of the line that are $b$ units wide. The dot in the middle is 0. I'm plotting values of $a$ from a region slightly bigger than $(-2b, 2b)$. As I mentioned above, different languages define modulo differently; the code for these figures was written in Processing, which compiles to Java.

The first image shows the results of a%b when $b$ is positive. Remember that $a$ is negative on the left side of the plot, and positive on the right.

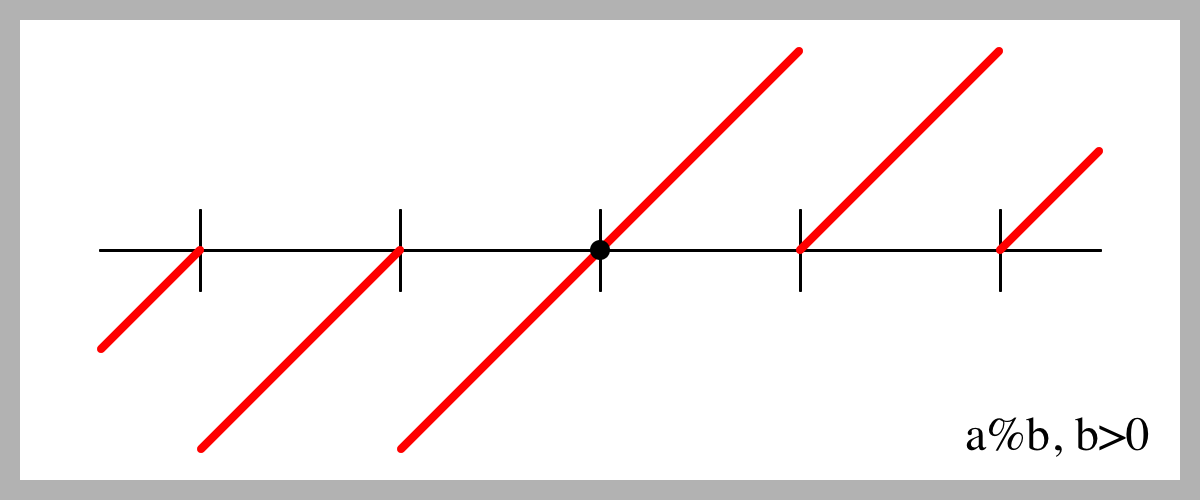
This plot reveals that the result of a%b is negative when the input is negative. In almost every program I've written, this is not what I want, so I have to test for this condition either before or after calling modulo, and manually patch things up. And notice we can't just make the negative values positive (they'd be sloping the wrong way). To get this to behave the way we want, we have to do a little computation. And so that we can use this just like modulo, we have to be careful to guarantee that nb%b=0 for all integer values of $n$.

Here's a plot of what wrap() returns, which satisfies those conditions and is almost always what I'm after.

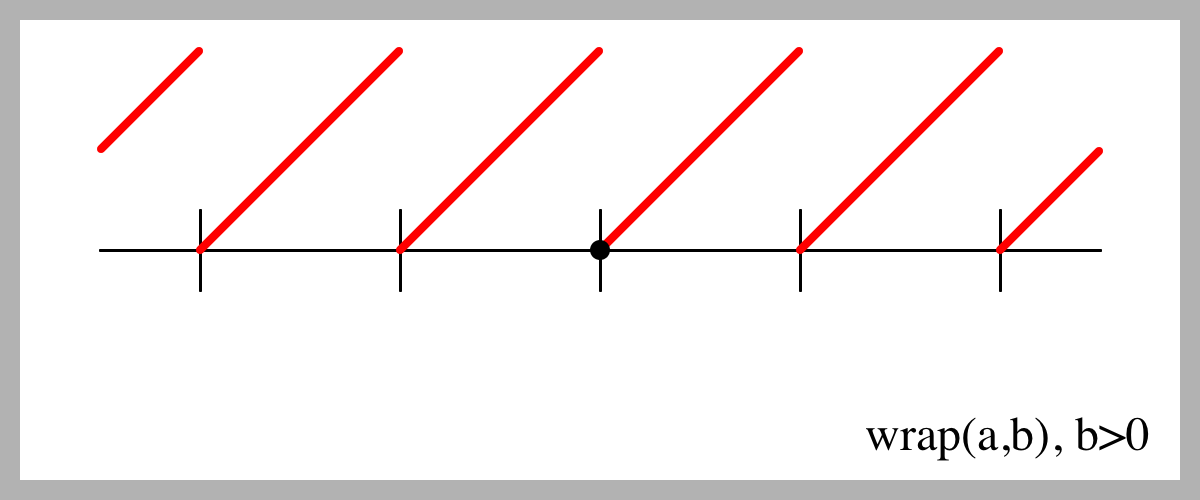
Nice. It's hard to tell from the picture, but it obeys the condition above: nb%b=0 for all integers n, even 0. Try printing out a few values if you want to check.

What if the modulus $b$ is less than zero? The next figure shows the results of modulo a%b for the same range of $a$, but a negative value of $b$.

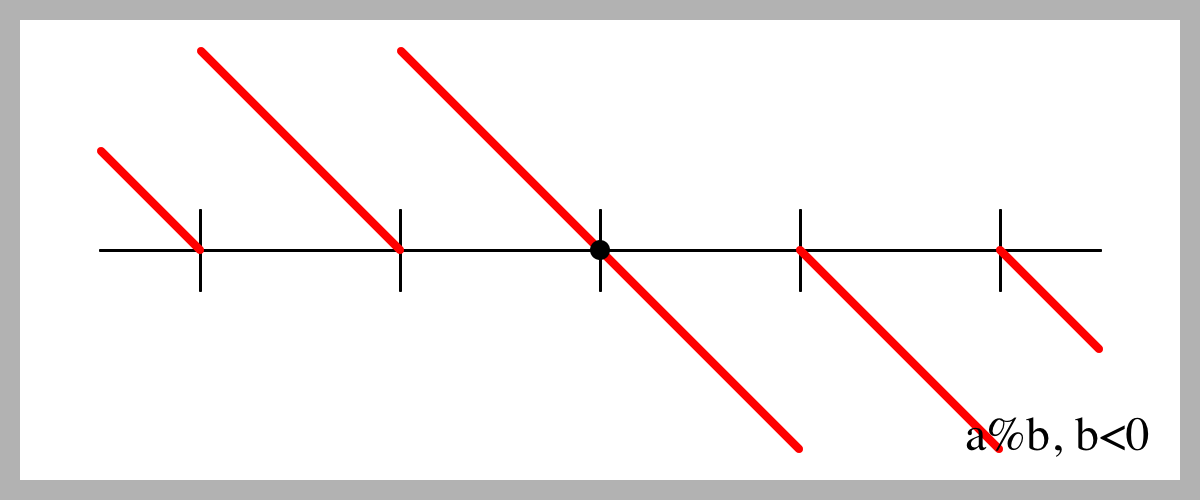
Again, sometimes it's positive, sometimes it's negative. But that's not what really bothers me here. The bigger issue for me is that the line slopes the wrong way in the region $[0, b)$.

Think of it this way. When $b$ is positive, then values of $a$ between 0 and b come out of a%b unchanged. In practice, I want the same thing to happen when $b$ is negative: values of $a$ between $0$ and $b$ (now negative) should also come out unchanged. This result shows that modulo doesn't do that.

So let's make that happen. Here's what wrap() returns when $b$ is negative.

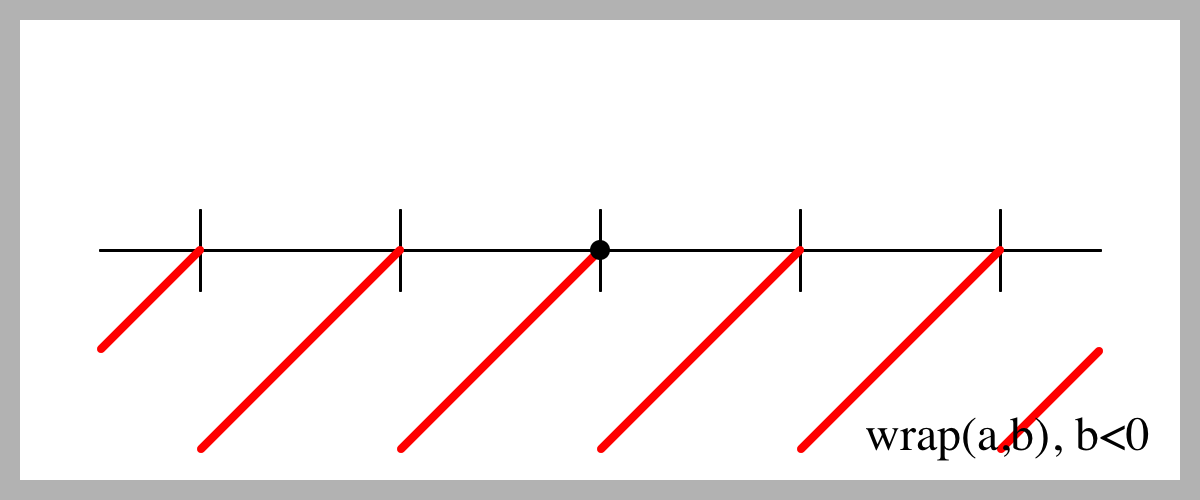
This is almost always what I want in those rare times when $b<0$.

Conclusion

When I want to compute a modulo-like operation, and I know for sure that both of my inputs are positive, I still use the built-in modulo operator %. It's fast and easy. But when there's even a chance that one or both values could be negative, I use wrap() instead. When both inputs are positive, it returns the same result as modulo. When either or both inputs are negative, it returns what I find to be the most useful result from a practical point of view.

Availability

An implementation of wrap() for the Processing environment is available in my open-source Andrew's Utilities Library. Just install it from Processing's built-in Library Manager and call AULib.wrap() instead of modulo.